Tangentes a círculos

Se calculan las ecuaciones de las siguientes tangentes a uno o dos círculos. Las construcciones se dibujan y las líneas de construcción se muestran si es necesario.

• La tangente a un círculo k en un punto B.
• Las tangentes a un círculo k a través de un punto P fuera del círculo
• Las tangentes a un círculo k paralelo a una línea recta g
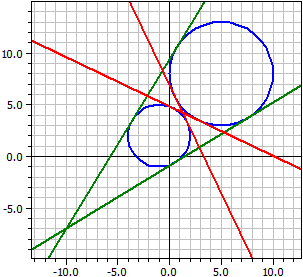
• Las tangentes a dos círculos k₁ y k₂ 

Ejemplo 1:

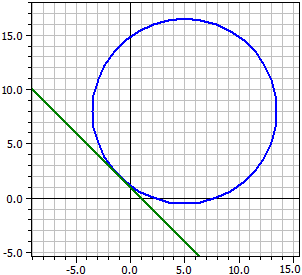
Dado : 
¯¯¯¯¯
k : M(5 | 8) ,   r =8,48528 ,    B(-1 | 2)   

Tangente a k en P 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t: x + y = 1

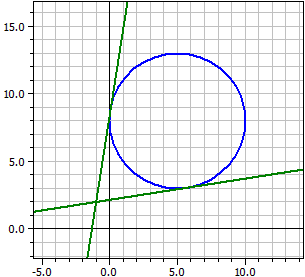
Ejemplo 2:

Dado : 
¯¯¯¯¯
k : M(5 | 8) ,   r =5 ,    P(-1 | 2)

Tangentes a k a través P 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: 1,06014·x − 6,77319·y = -14,6065
  t2: 6,77319·x − 1,06014·y = -8,89348

Puntos de contacto 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  k n t1 = B1(5,77319|3,06014)
  k n t2 = B2(0,0601439|8,77319)

Polar 
¯¯¯¯¯
  p : 6·x + 6·y = 53

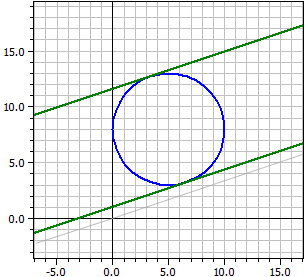
Ejemplo 3:

Dado : 
¯¯¯¯¯
  k : M(5 | 8) ,   r =5 ,      g : -x + 3·y = 0

Tangentes a k paralelas a g 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: x − 3·y = -3,18861
  t2: x − 3·y = -34,8114

Puntos de contacto 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  k n t1 = B1(6,58114|3,25658)
  k n t2 = B2(3,41886|12,7434)

Línea perpendicular 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  Lot: 3·x + y = 23

Ejemplo 4:

Dado : 
¯¯¯¯¯
  k1 : M(5|8) ,   r =5
  k2 : M(-1|2) ,   r =3

Tangentes exteriores 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t1: -4,2923·x + 7,04104·y = -6,36427
  t2: -7,04104·x + 4,29230·y = 40,3643

Tangentes interiores 
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
  t3: 1,21895·x + 2,55228·y = 12,3709
  t4: -2,55228·x − 1,21895·y = -8,3709

Ver también:

Wikipedia: Rectas tangentes a circunferencias