Líneas especiales en un triángulo
Si se introducen las coordenadas de las tres vértices de un triángulo, el programa calcula las ecuaciones de los mediatrices[1], de los medianas[2], de los bisectrices[3] y de las alturas[4]. Además, los centros y radios del círculo inscrito[5], del círculo circunscrito[6], de los círculos tangenciales[7] y del círculo de Feuerbach[8].
Se puede utilizar una lista de casillas de verificación para seleccionar qué objetos deben calcularse y dibujarse.
 Mediatrices
Mediatrices
 Medianas
Medianas
 Bisectrices
Bisectrices
 Alturas
Alturas
 Círculo inscrito
Círculo inscrito
 Círculo circunscrito
Círculo circunscrito
 Círculos tangenciales
Círculos tangenciales
 Círculo de Feuerbach
Círculo de Feuerbach
Ejemplo 1: Círculo inscrito y círculos tangenciales de un triángulo
Dado :
¯¯¯¯¯
Vértices : A(1|0) B(5|1) C(3|6)
Resultados
¯¯¯¯¯¯¯¯¯
Lados : a : 5·x + 2·y = 27
b : 3·x - y = 3
c : x − 4·y = 1
Círculo inscrito : Mi(3,119|1,962) r i = 1,390
Círculos tangenciales : Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
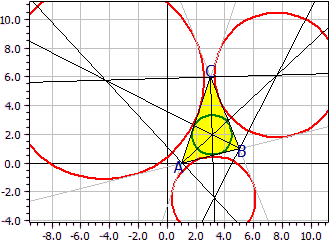
El centro del círculo inscrito (verde) se encuentra en el bisector de los tres ángulos interiores. Los centros de los círculos tangenciales (rojo) están cada uno en el bisector de un ángulo interior y en el bisector del ángulo exterior de los otros dos ángulos triangulares. Estas líneas de construcción también se dibujan.
Ejemplo 2: Alturas en un triángulo obtuso
Dado :
¯¯¯¯¯
Vértices : A(7|3) B(16|10) C(8|9)
Resultados
¯¯¯¯¯¯¯¯¯
Lados : a : -x + 8·y = 64
b : 6·x - y = 39
c : 7·x − 9·y = 22
Alturas : ha : 8·x + y = 59
hb : x + 6·y = 76
hc : 9·x + 7·y = 135
Puntos de plomada : Ha(6,277|8,785) Hb(8,378|11,27)
Hc(10,53|5,746)
Intersec. de las alturas : H(11,05|8,26)
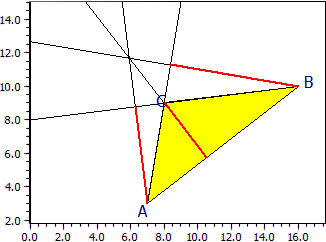
La intersección de las alturas de un triángulo obtuso se encuentra fuera del triángulo. También se trazan las líneas de construcción. Para hacerlos más visibles, las líneas de la cuadrícula se han ocultado.
Ejemplo 3: Los círculos tangenciales y el círculo de Feuerbach
Dado:
¯¯¯¯
Vértices : A(1|0) B(5|1) C(3|6)
Resultados:
¯¯¯¯¯¯¯¯¯
Lados: a : 5·x + 2·y = 27
b : 3·x − y = 3
c : x − 4·y = 1
Círculos tangenciales: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
Círculo de Feuerbach: M9(3,295|2,068) r9 = 1,596
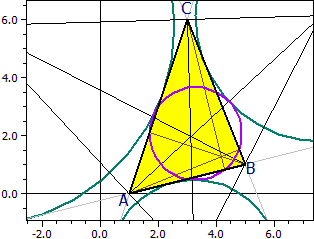
El círculo de Feuerbach toca al círculo inscrito y al círculos tangenciales (teorema de Feuerbach).
Ver también:
Ajuste de los gráficos
Wikipedia:
Circunferencia inscrita y exinscrita en un triángulo |
Circunferencia de los nueve puntos


