Newton-Iteration

Newton's iteration is an approximation method for the calculating a zero of ƒ(x). Given an initial value x0 that is close enough to the desired zero, the next approximation is the intersection of the tangent to the graph of ƒ in the point P(x0|ƒ(x0)) with the x-axis.

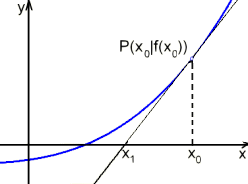
This gives the recursion formula

    xn + 1  = xn  - ƒ (xn) / ƒ '(xn)

The procedure converges, if  ƒ(x0) · ƒ "(x0)>0
is valid for x0.

Example:

  ƒ(x) = x-cos(x)

                 x                       ƒ(x)                  ƒ'(x) 
   ————————   ——————   ——————   
   x0 = 1
   x1 = 0,75036387     0,45969769       1,841471
   x2 = 0,73911289     0,018923074     1,681905
   x3 = 0,73908513     0,00004646       1,6736325
   x4 = 0,73908513     0,00000000       1,673612

See also:

Supported Functions
Wikipedia: Newton's method