Normalverteilung

Die Normalverteilung beschreibt eine Verteilung, bei der Werte um den Mittelwert  μ  herum am häufigsten vorkommen und die Wahrscheinlichkeit von Werten abnimmt, je weiter sie vom Mittelwert entfernt sind.
Die Dichtefunktion  ƒ  der Normalverteilung, charakterisiert durch den Erwartungswert  μ  und die Varianz  σ², ist symmetrisch und hat die Form einer Glockenkurve. Die Verteilungsfunktion  Φ , auch als Gaußsche Fehlerfunktion bekannt, gibt die Wahrscheinlichkeit an, dass eine Zufallsvariable einen Wert kleiner oder gleich einem bestimmten Wert annimmt.

Berechnet werden für eine  N(μ,σ²) verteilte Zufallsgröße  X  mit gegebenem Erwartungswert μ und Varianz  σ²

 

- die Dichtefunktion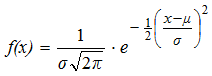    

- und die Verteilungsfunktion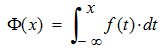

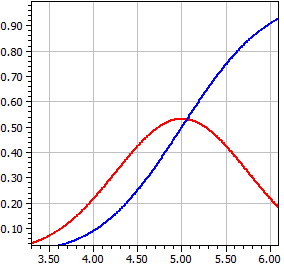
Das Schaubild der Dichtefunktion  ƒ  wird oft als Gauß-Kurve oder wegen seiner Form als Glockenkurve bezeichnet. Die Verteilungsfunktion  Φ  heißt auch Gauß-Fehlerfunktion, da man nach Gauß für die zufälligen Fehler astronomischer Beobachtungen diese Verteilung annimmt.

Eingegeben werden der Erwartungswert  μ  und die Varianz  σ². Für  μ=0  und  σ=1  erhält man die standardisierte Normalverteilung.

Beispiel

  μ = 5 ,      σ = .75

         x                     ƒ(x)                   Φ(x)      
  —————       –—————     —————–
  2                       0,00017844      0,00003167   
  2,33333333      0,00095649      0,00018859
  2,66666666      0,00420802      0,00093192
  2,99999999      0,01519465      0,00383038
  3,33333332      0,04503153      0,01313415
  3,66666665      0,10953585      0,03772017
  3,99999998      0,21868009      0,09121120
  4,33333331      0,35832381      0,18703139
  4,66666664      0,48189843      0,32836063
  4,99999997      0,53192304      0,49999998
  5,3333333        0,48189845      0,67163934
  5,66666663      0,35832383      0,81296859
  5,99999996      0,21868012      0,90878878
  6,33333329      0,10953586      0,96227982

Siehe auch:

Einstellen der Grafik
Wikipedia: Normalverteilung