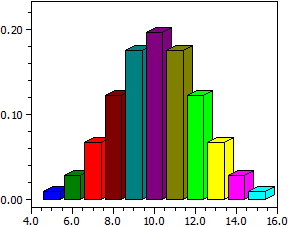
Hypergeometrische Verteilung

Die hypergeometrische Verteilung beschreibt Situationen, in denen Objekte ohne Zurücklegen aus einer endlichen Menge gezogen werden. Die Besonderheit dieser Verteilung liegt in der Abhängigkeit der Ziehungen voneinander, da sich die Zusammensetzung der Urne nach jeder Ziehung ändert.

Berechnet werden für eine h(k;n;m;r) verteilte Zufallsgröße X bei festem n, m und festem r ein Stabdiagramm und eine Wertetabelle für die Wahrscheinlichkeiten P( X = k ).

Die Routine ist besonders nützlich, da wegen der vier Eingabegrößen kaum Tabellen für die hypergeometrische Verteilung existieren und die Berechnung der Wahrscheinlichkeiten sehr aufwendig ist.

Theorie:

Eine Urne enthält m Kugeln, von denen r rot sind. Werden n Kugeln ohne Zurücklegen gezogen, so gibt die Zufallsgröße X an, wie viel rote Kugeln gezogen wurden. Die Wahrscheinlichkeit, dass k der gezogenen Kugeln rot sind, wird mit P(X=k) = h(k,n,m,r) bezeichnet.

Eingegeben werden die Zahl der gezogenen Kugeln n, die Gesamtzahl m und die Anzahl der roten Kugeln r. Da ohne Zurücklegen gezogen wird, muss n<m sein, außerdem natürlich r<m.

Beispiel:

  n = 20;    m = 100;    r = 50

     k         P(X=k)            P(0 ≤ X < k)
  ——   ——————    ——————
     5       0,00889760      0,01141749 
     6       0,02780501      0,03922250 
     7       0,06613084      0,10535334 
     8       0,12160243      0,22695577 
     9       0,17460862      0,40156439 
    10      0,19687122      0,59843561 
    11      0,17460862      0,77304423 
    12      0,12160243      0,89464666 
    13      0,06613084      0,96077750 
    14      0,02780501      0,98858251 
    15      0,00889760      0,99748011 
  ——   ——————    ——————
  P(5 ≤ k < 15) =             0,99496023

Siehe auch:

Wikipedia: Hypergeometrische Verteilung