Binomialverteilung
Die Binomialverteilung beschreibt die Wahrscheinlichkeit des Auftretens einer festen Anzahl k von Erfolgen in einer Folge von n unabhängigen Versuchen, bei denen nur zwei mögliche Ergebnisse existieren.
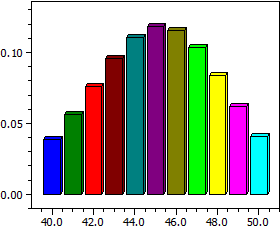
Berechnet werden für eine b(k;n;p) verteilte Zufallsgröße X bei festem n und festem p ein Stabdiagramm der Wahrscheinlichkeiten
Theorie:
Aus einer Urne mit einem Anteil von p roten Kugeln werden n Kugeln mit Zurücklegen gezogen. Die Zufallsgröße X gibt an, wie viel rote
Kugeln gezogen wurden. Die Wahrscheinlichkeit, dass k der gezogenen Kugeln rot sind, wird mit
Eingegeben werden die Werte für n und p, wobei p als Wahrscheinlichkeit zwischen 0 und 1 liegen muss. Danach gibt ein einfaches Stabdiagramm
einen ersten Überblick über die Werte von
Beispiel:
n = 60; p = .75
k P(X=k) P(0 ≤ X < k)
—— —————— ——————
40 0,03834033 0,09248427
41 0,05610780 0,14859207
42 0,07614630 0,22473838
43 0,09562559 0,32036397
44 0,11083875 0,43120273
45 0,11822800 0,54943073
46 0,11565783 0,66508856
47 0,10335381 0,76844237
48 0,08397497 0,85243
49 0,06169589 0,91411323
50 0,04071929 0,95483252
—— —————— ——————
P(40 ≤ k < 50) = 0,90068858