Kombinatorik

Berechnet werden die Anzahlen der Möglichkeiten, aus n Elementen k auszuwählen, wenn auf die Reihenfolge Wert gelegt wird oder nicht und wenn Wiederholungen zugelassen sind oder nicht.

Beispiel:

n = 49 ,  k = 6

Geordnete Auswahl ohne Wiederh.= 10 068 347 520
Geordnete Auswahl mit  Wiederh.  = 13 841 287 201
Ungeordnete Ausw. ohne Wiederh.= 13 983 816          (Lotto)
Ungeordnete Ausw. mit  Wiederh.  = 25 827 165

Permutationen von k :                k ! = 720

Die ungeordnete Auswahl ohne Wiederholung liegt beispielsweise beim Zahlenlotto "6 aus 49" vor. Das heißt wir erhalten die  13 983 816  Möglichkeiten von 49 Feldern 6 anzukreuzen.

Formeln:

	Ungeordnet (Kombinationen)	Geordnet (Variationen)	Geordnet und k=n (Permutationen)
Ohne Wiederholungen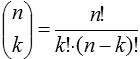
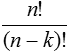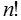Mit Wiederholungen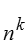

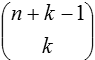Beim Urnenmodell entspricht die Auswahl mit Wiederholungen dem Ziehen mit Zurücklegen, die ohne Wierholungen dem Ziehen ohne Zurücklegen. Der geordneten Auswahl entspricht, dass die Kugeln einzeln gezogen werden, der ungeordneten Auswahl, dass sie gleichzeitig gezogen werden.

Siehe auch:

Wikipedia: Abzählende Kombinatorik