MatheAss 10.0 − Geometrie 2D

Besondere Geraden im Dreieck

Werden von einem Dreieck die Koordinaten der drei Eckpunkte eingegeben, berechnet das Programm die Gleichungen der Mittelsenkrechten[1], der Seitenhalbierenden[2]. der Winkelhalbierenden[3] und der Höhen[4]. Außerdem die Mittelpunkte und Radien des Umkreises[5], des Inkreises[6], der drei Ankreise[7] und des Feuerbachkreises[8].

In einer Liste von Check Boxes kann ausgewählt werden, welche Größen berechnet und gezeichnet werden sollen.

Mittelsenkrechte
Seitenhalbierende
Winkelhalbierende
Höhen
Inkreis
Umkreis
Ankreise
Feuerbachkreis

Beispiel 1: Inkreis und Ankreise eines Dreiecks

Gegeben:
¯¯¯¯¯¯¯¯
       Ecken:    A(1|0)   B(5|1)   C(3|6)
 
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
      Seiten:   a :  5·x + 2·y = 27
                    b :  3·x - y = 3
                    c :  x - 4·y = 1
 
     Inkreis:    Mi(3,119|1,962)         r i = 1,390
 
  Ankreise:    Ma(7,626|6,136)       ra = 4,346
                     Mb(-4,356|5,784)      rb = 6,910
                     Mc(3,248|-2,427)      rc = 2,900

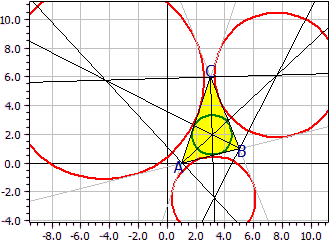
Der Mittelpunkt des Inkreises (grün) liegt auf den Winkelhalbierenden der drei Innenwinkel. Die Mittelpunkte der Ankreise (rot) liegen jeweils auf der Winkelhalbierenden eines Innenwinkels und auf den Winkelhalbierenden der Außenwinkel der beiden anderen Dreieckswinkel. Diese Konstruktionslinien werden mit eingezeichnet.

Beispiel 2: Höhen in einem stumpfwinkligen Dreieck

Gegeben:
¯¯¯¯¯¯¯¯
       Ecken:  A(7|3)   B(16|10)  C(8|9)
 
Ergebnisse:
¯¯¯¯¯¯¯¯¯¯
       Seiten:   a : -x + 8·y = 64
                     b : 6·x - y = 39
                     c : 7·x - 9·y = 22
 
       Höhen:  ha : 8·x + y = 59
                    hb : x + 6·y = 76
                    hc : 9·x + 7·y = 135
  
Lotfußpkte: Ha(6,277|8,785)  Hb(8,378|11,27)
	           Hc(10,53|5,746

Höhenschnittpunkt: H(11,05|8,26)

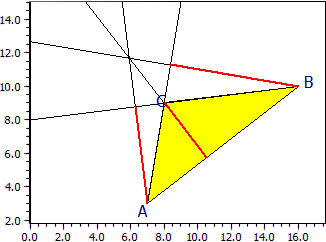
Der Schnittpunkt der Höhen liegt beim stumpfwinkligen Dreieck außerhalb des Dreiecks. Die Konstruktionslinien werden mit eingezeichnet. Um sie besser sichtbar zu machen, wurden die Gitterlinien ausgeblendet.

Beispiel 3: Ankreise und Feuerbachkreis

Gegeben:
¯¯¯¯¯¯¯¯       
             Ecken:    A(1|0)   B(5|1)   C(3|6)
 
Ergebnisse
¯¯¯¯¯¯¯¯¯¯
             Seiten:   a :  5·x + 2·y = 27
                           b :  3·x − y = 3
                           c :  x − 4·y = 1
 
          Ankreise:   Ma(7,626|6,136)      ra = 4,346
                            Mb(-4,356|5,784)     rb = 6,910
                            Mc(3,248|-2,427)     rc = 2,900
							  
Feuerbachkreis:  M9(3,295|2,068)      r9 = 1,596

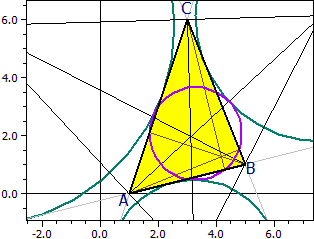
Der Feuerbachkreis berührt den Inkreis und die Ankreise (Satz von Feuerbach).

Siehe auch:

Einstellen der Grafik
Wikipedia: Ankreis | Feuerbachkreis

[1]  Die Mittelsenkrechten sind die Geraden. die jeweils eine Dreieckseite im Mittelpunkt senkrecht schneiden. Ihr Schnittpunkt ist der Mittelpunkt des Umkreises.
[2]  Die Seitenhalbierenden sind die Strecken von jeweils einem Eckpunkt des Dreiecks zur Mitte der gegenüberliegenden Seite. Ihr Schnittpunkt ist der Schwerpunkt des Dreiecks.
[3]  Die Winkelhalbierenden halbieren, wie ihr Name schon sagt, jeweils einen der Innenwinkel des Dreiecks. Ihr Schnittpunkt ist der Mittelpunkt des Inkreises des Dreiecks.
[4]  Die Höhen sind die Lotgeraden von jeweils einer Ecke des Dreiecks auf die gegenüber liegende Seite. Ihr Schnittpunkt wird auch das Orthozentrum des Dreiecks gennant.
[5]  Der Umkreis eines Dreicks ist der Kreis durch die Eckpunkte des Dreiecks. Sein Mittelpunkt liegt beim spitzwinkligen Dreick innerhalb, beim stumpfwinkligen Dreieck außerhalb des Dreiecks.
[6]  Der Inkreis ist der Kreis, der die drei Seiten des Dreiecks von innen berührt. Sein Mittelpunkt ist der Schnittpunkt der Winkelhalbierenden.
[7]  Die Ankreise berühren jeweils eine Dreieckseite von außen und werden von den Verlängerungen der beiden anderen Seiten tangential berührt.
[8]  Auf dem Feuerbachkreis oder Neun-Punkte-Kreis eines Dreiecks, liegen die Mittelpunkte der Seiten, die Fußpunkte der Höhen und die Mittelpunkte der oberen Höhenabschnitte. Außerdem berührt er die drei Ankreise.

Impressum www.matheass.eu