Calcolo integrale
Vengono calcolate la superficie orientata e la superficie assoluta tra due curve in un intervallo scelto.
Inoltre, il programma determina:
- I momenti di rotazione attorno agli assi x e all'asse y,
- i corpi della rivoluzione,
- le lunghezze d'arco nell'intervallo [a;b] e
- il centro di gravità dell'area (se A1=A2).
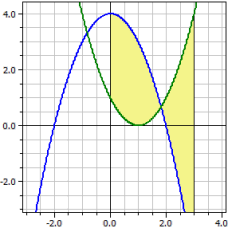
Esempio 1:
ƒ1(x) = 4-x^2 ƒ2(x) = (x-1)^2 Intervallo di integrazione da 0 a 3 Superficie orientata : A1 = 0,00000 Superficie assoluta : A2 = 9,50675 Momenti di rotazione : Mx = 9 My = -9 Corpi di rivoluzione : Vx = 56,5487 Vy = -56,5487
Esempio 2:
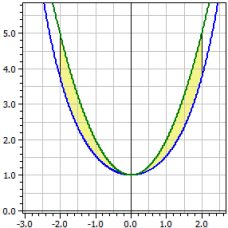
Lunghezza dell'arco della linea catena rispetto alla parabola normale y=x2+1.
ƒ1(x) = cosh(x) ƒ2(x) = x^2+1 Intervallo di integrazione da -2 a 2 Superficie orientata : A1 = -2,07961 Superficie assoluta : A2 = 2,07961 Lunghezze dell'arco : L1[a;b] = 7,254 L2[a,b] = 9,294
Notare che:
Gli integrali sono determinati usando metodi numerici. In linea di principio, questi raggiungono i loro limiti con funzioni con un cambio di segno molto veloce.
Vedi anche:
Funzioni supportateImpostazioni delle grafiche

