Studio di funzioni polinomiali

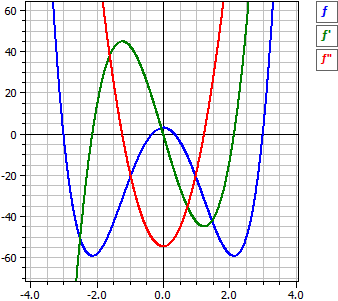
Il programma svolge la discussione sulla curva di una funzione polinomiale. Ciò significa che vengono determinati i derivati e la funzione primitiva, la funzione viene esaminata per zeri razionali, per estremi, per punti di svolta e per simmetria. Vengono disegnati i diagrammi di  ƒ, ƒ'  e  ƒ"  e  viene emessa una tabella di valori.

I coefficienti del polinomio possono essere inseriti come frazioni, come frazioni misti o come numeri decimali.

Se si immettono limiti di intervallo per un integrale, il valore dell'integrale specifico su questo intervallo viene determinato oltre all'antiderivativo.

Tutte le parti del programma in cui vengono immessi i coefficienti di un polinomio hanno un menù contestuale (pulsante destro del mouse) con il quale è possibile copiare le i coefficienti da una parte del programma negli Appunti di Windows  e incollarle da lì in un'altra parte del programma.

Esempio

Funzione:
¯¯¯¯¯¯¯¯
  ƒ(x) = 3·x4 - 82/3·x2 + 3
       = 1/3·(9·x4 - 82·x2 + 9)
       = 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)

Derivazioni:
¯¯¯¯¯¯¯¯¯¯
  ƒ'(x)  = 12·x3 - 164/3·x
  ƒ"(x)  = 36·x2 - 164/3
  ƒ'"(x) = 72·x

Primitiva:
¯¯¯¯¯¯¯
  F(x) = 3/5·x5 - 82/9·x3 + 3·x + c

Zeri:
¯¯¯¯
  N1( 1/3 | 0)                             m = -17,7778
  N2(-1/3 | 0)                             m =  17,7778
  N3( 3 | 0)                                m =  160
  N4(-3 | 0)                                m = -160

Estremi:
¯¯¯¯¯¯¯
  H1( 0 | 3)                                m =  0
  T1(-2,13437 |-59,2593)          m =  0
  T2( 2,13437 |-59,2593)          m =  0

Punti di flesso:
¯¯¯¯¯¯¯¯¯¯¯¯
  W1(-1,23228 |-31,5885)        m =  44,9098
  W2( 1,23228 |-31,5885)        m = -44,9098

Simmetria:
¯¯¯¯¯¯¯¯¯
  Assialmente simmetrico a  a: x =0

Vedi anche: