Successiones e Series
Il programma determina i primi n termini di una successione (ai) e la serie associata (somma dei termini della successione) se i primi termini della successione e una funzione esplicita ai=ƒ(i) o una formula di ricorso ai=ƒ(a0, a1, ... , ai-1) sono dati.
La successione dei numeri dispari
Può essere definito esplicitamente da ai = 2·i + 1 :
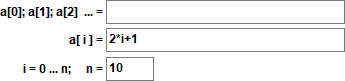
o ricorsivamente da ai = ai-1 + 2 con a0=1 .

Successione ¯¯¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
La serie corrispondente è ovviamente la successione dei numeri quadrati. Questo può essere dimostrato molto bene per induzione completa.
La successione di Fibonacci
Una delle sequenze ricorsive più popolari inizia con a0=1 e a1=1 . Gli altri termini sono uguali alla somma dei due precedenti.

Successione ¯¯¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Vedi anche:
Wikipedia: Successione (matematica) | Successione di Fibonacci

