Intersezione di due piani
Per due piani, il programma determina la retta di intersezione, la distanza di origine dalla retta e l'angolo tra i due piani.
I piani possono essere immessi nella rappresentazione parametrica o nell'equazione delle coordinate
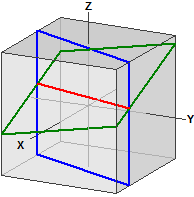
Sono designate le intersezioni del piano con un cubo simmetrico agli assi e le rette di intersezione dei due piani.
Esempio 1:
I due piani:
¯¯¯¯¯¯¯¯¯¯¯
E1: 5·x - 2·y = 5
E2: 2·x - y + 5·z = 8
La retta di intersezione:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧-11 ⎫ ⎧ 10 ⎫
g : x = ⎪-30 ⎪ + r·⎪ 25 ⎪
⎩ 0 ⎭ ⎩ 1 ⎭
La distanza dall'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1.5057283
L'angolo tra i piani:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
alfa = 65.993637°
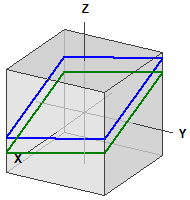
Esempio 2: Parallele Ebenen
I due piani: ¯¯¯¯¯¯¯¯¯¯¯ E1 : 2·x - y + 5·z = 12 E2 : 2·x - y + 5·z = 0 I piani sono parallele ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ d(E1,E2) = 2,1908902
È possibile ruotare il diagramma con il tasto sinistro del mouse e ingrandire con il tasto destro del mouse.

