Piano tra tre punti
Tre punti nello spazio, che non sono allineati, determinano solo un piano. Le coordinate dei tre punti dati, il programma determina l'equazione del piano rappresentato da un punto e due vettori di direzione. E l'equazione in coordinate. Oltre alla distanza dall'origine. I vettori guida e il vettore normale sono estesi a numeri interi.
Inoltre, la posizione del piano nello spazio è illustrata da una proiezione obliqua. Contiene le rette di intersezione con un cubo, simmetrico agli assi e ai punti di traccia.
Esempio:
Piano attraverso i punti:
A(1|2|3), B(2|3|3), C(1|0|1)
L'equazione vettoriale:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
L'equ. in coordinate:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Distanza dall'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Punti di traccia:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx (2|0|0)
Sy (0|-2|0)
Sz (0|0|2)
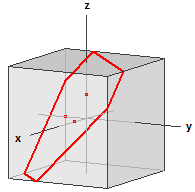
È possibile ruotare il diagramma con il tasto sinistro del mouse e ingrandire con il tasto destro del mouse.

