Poligoni arbitrari
Innanzitutto devono essere inserite le coordinate dei punti dei vertici di un poligono.
Successivamente, vengono visualizzate l'area, la circonferenza e le coordinate dei centri di gravità (rispettivamente nei punti o nell'area) e viene disegnato il poligono.
Vengono calcolati anche i lati e gli angoli del poligono e viene verificato se il poligono è convesso, concavo o intrecciato.
Poligono convesso:
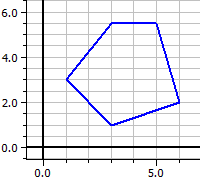
Poligono concavo:
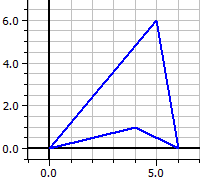
Poligono intrecciato:
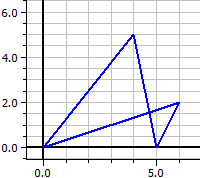
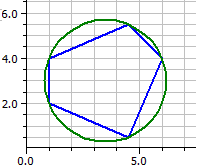
Inoltre, i poligoni convessi vengono controllati se hanno un cerchio inscritto e/o un cerchio circoscritto.
Poligono tangente:
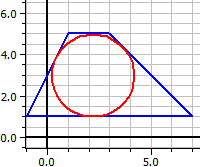
Poligono ciclico:
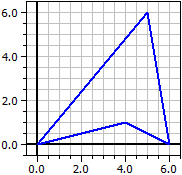
Esempio:
Vertici: Area A = 18
A (0 | 0)
B (4 | 1) Circonferenza p = 22.032567
C (6 | 0)
D (5 | 7) Baricentro di vertici:
CP (3,75 | 2)
Baricentro di area:
CA (3,72,222 mila | 2.66667)
Lati: Angoli:
|AB| = 4,1231056 ∡BAD = 36,158185°
|BC| = 2,236068 ∡CBA = 220,60129°
|CD| = 6,0827625 ∡DCB = 53,972627°
|DA| = 7,8102497 ∡ADC = 49,267893°
Konkaves Vieleck
∡BAD è l'angolo di cui il raggio [AB[ viene
ruotato in senso antiorario fino a [AD[.

