Étude des fonctions polynômiales

Le programme effectue la discussion de la courbe pour une fonction polynômiale. Cela signifie que les dérivées et l'antidérivatif sont déterminées, la fonction est examinée pour les zéros rationnels, pour les extrêmes, pour les points de retournement et pour la symétrie. Les diagrammes de f, f 'et f "sont dessinés et un tableau de valeurs est sorti.

Les coefficients du polynôme peuvent être entrés sous forme de fractions, de nombres mixtes ou de nombres décimaux décomposés.

Si des limites d'intervalle pour une intégrale sont entrées, la valeur de l'intégrale spécifique sur cet intervalle est déterminée en plus de la primitive.

Exemple

Fonction:
¯¯¯¯¯¯¯
ƒ(x) = 3·x4 - 82/3·x2 + 3
       = 1/3·(9·x4 - 82·x2 + 9)
       = 1/3·(3·x - 1)·(3·x + 1)·(x - 3)·(x + 3)

Les dérivées:
¯¯¯¯¯¯¯¯¯¯¯
ƒ'(x)  = 12·x3 - 164/3·x
ƒ"(x)  = 36·x2 - 164/3
ƒ'"(x) = 72·x

L'antidérivatif:
¯¯¯¯¯¯¯¯¯¯¯
F(x) = 3/5·x5 - 82/9·x3 + 3·x + c

Les zéros:
¯¯¯¯¯¯¯¯
N1( 1/3 | 0)                             m = -17,7778
N2(-1/3 | 0)                             m =  17,7778
N3( 3 | 0)                                m =  160
N4(-3 | 0)                                m = -160

Les extrema:
¯¯¯¯¯¯¯¯¯¯
H1( 0 | 3)                                m =  0
T1(-2,13437 |-59,2593)          m =  0
T2( 2,13437 |-59,2593)          m =  0

Pts d'inversions:
¯¯¯¯¯¯¯¯¯¯¯¯¯
W1(-1,23228 |-31,5885)        m =  44,9098
W2( 1,23228 |-31,5885)        m = -44,9098

Symétrie:
¯¯¯¯¯¯¯¯
  Axialsymétrique à  a: x =0

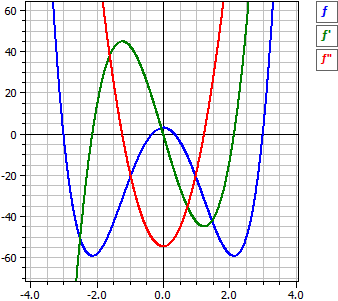
   Avec les interrupteurs sur le bord droit, les courbes de ƒ, ƒ'
   et ƒ" peuvent être activées et désactivées individuellement.

Toutes les parties de programme dans lesquelles les coefficients d'un polynôme sont entrés ont un menu contextuel (bouton droit de la souris) avec lequel vous pouvez copier les entrées d'une partie de programme dans le presse-papiers et les coller à partir de là dans une autre partie de programme.

Voir aussi: