Suites et Séries
Le logiciel détermine les n premiers termes d'une suite (ai) ainsi que ceux de la série associée (somme des termes de la suite), lorsqu’une fonction explicite ou les premiers termes de la suite accompagnés d’une règle de récurrence ai=ƒ(a0, a1, ... , ai-1) sont fournis.
La suite des nombres impairs
Il peut être défini explicitement par ai = 2·i + 1 :
a[0] ... =
a[ i ] = 2*i + 1
n = 10
a[i] = 2*i + 1; n = 10; Suite ¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Série ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
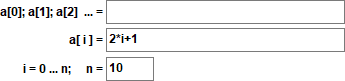
ou récursivement par ai = ai-1 + 2 with a0=1 .
a[0] ... = 1
a[ i ] = a[i-1]+2
n = 10
a[0] = 1; a[i] = a[i-1]+2; n = 10; Suite ¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Série ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
La série correspondante est évidemment la suite des nombres carrés. Cela peut être prouvé très bien par induction complète. ( Wikipedia: Raisonnement_par_récurrence / Exemple 1 : la somme des n premiers entiers impairs )
La suite de Fibonacci
L'une des suite récursives les plus populaires commence par a0=1 et a1=1 . Les autres termes sont égaux à la somme des deux précédents.
a[0] ... = 1; 1
a[ i ] = a[i-1]+a[i-2]
n = 20
a[0]=1; a[1]=1; a[ i ] = a[i-1]+a[i-2]; n = 20 Suite ¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Série ¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Voir aussi:
Wikipedia: Suite