Plan à travers trois Points
Trois points dans l'espace, qui ne sont pas alignés, détermine uniquement un plan. Les coordonnées des trois points donnés, le programme détermine l'équation du plan représenté par un point et deux vecteurs directeurs. Et l'équation en coordonnées. Ainsi que la distance de l'origine. Les vecteurs directeurs et le vecteur normal sont étendus aux nombres entiers.
En supplément, la position du plan dans l'espace est illustré par une projection oblique. Elle contient les droites d'intersections avec un cube, symétrique aux axes et les points de trace.
Exemple:
Plan à travers
A(1|2|3), B(2|3|3), C(1|0|1)
L'équation vectoriel:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
-> ⎧ 1 ⎫ ⎧ 1 ⎫ ⎧ 0 ⎫
x = ⎪ 2 ⎪ + r·⎪ 1 ⎪ + s·⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 0 ⎭ ⎩ 1 ⎭
L'équ. en coordonées:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
x - y + z = 2
Distance de l'origine:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
d = 1,1547005
Points de trace:
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Sx(2|0|0)
Sy(0|-2|0)
Sz(0|0|2)
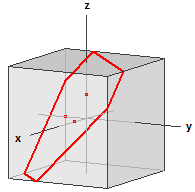
Vous pouvez tourner le diagramme avec le bouton gauche de la souris et faire un zoom avec le bouton droit de la souris.

