Ejemplo 2: Pandemia de Corona
Por supuesto, tiene sentido utilizar los datos actuales sobre la pandemia de corona para la regresión logística.
Tomé los datos para alemania del sitio web de la Universidad Johns Hopkins (JHU) , que se actualiza a diario, y los guardé en archivos CSV.
Datos de: "JHU_DE_Mrz-Apr.csv"
Límite de saturación: 56 Mio
Figura oscura: 1
4.5589 · 1010
ƒ (x) = ———————————————————
814,09 + 5,5999 · 107 · e ^ (- 0,11206 · t)
Punto de inflexión W(99,4 | 28 Mio)
Tasa máxima de crecimiento ƒ'(xw) = 1,5688 Mio
60 Valores
Coeficiente de determinación = 0,82574762
Coeficiente de correlación = 0,90870656
Desviación estándar = 0,90673232
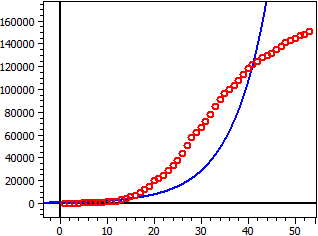
Datos de Alemania marzo-abril 2020, S=56 Mio, Figura oscura=1.
Datos de: "JHU_DE_Mrz-mai.csv"
Límite de saturación: 56 Mio
Figura oscura: 300
2,5497 · 1013
ƒ(x) = ———————————————————
4,553·105 + 5,5545·107·e^(- 0,10581 · t)
Punto de inflexión W (45,404 / 28 Mio)
Tasa máxima de crecimiento ƒ '(xw ) = 1,4813 Mio
92 Valores
Coeficiente de determinación = 0,90140376
Coeficiente de correlación = 0,94942285
Desviación estándar = 0,93956073
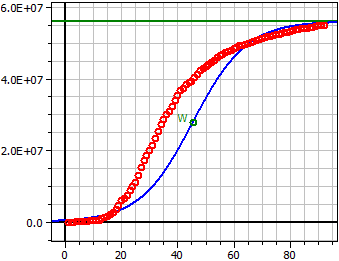
Datos de Alemania marzo-mayo 2020, S=56 Mio, Figura oscura=300.
Con valores grandes, la escala cambia al formato de número científico. 4.0E+07 = 4.0·107 = 40,000,000.
Supuse 56 millones como límite de saturación. Eso es el 70% de los 80 millones (Residentes en Alemania), el caso de la supuesta inmunidad colectiva .

