Cálculo integral
Se calculan el contenido orientado y absoluto del área entre dos curvas de función en un intervalo deseado, es decir, las dos integrales.
También se determinan:
- los momentos de torsión para la rotación alrededor del eje x, respectivamente y
- los cuerpos de la revolución cubiertos y
- las longitudes de arco en el intervalo [a; b] y
- el centro de gravedad del área (si A1 = A2).
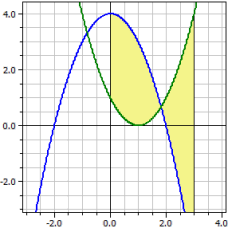
Ejemplo 1:
ƒ1 (x) = 4-x^2
ƒ2 (x) = (x-1)^2
Intervalo de von 0 a 3
Contenido orientado: A1 = 0,00000
Contenido absoluto: A2 = 9,50675
Momentos de torsión: Mx = 9 My = -9
Cuerpos de revolución: Vx = 56,5487
Vy = -56,5487
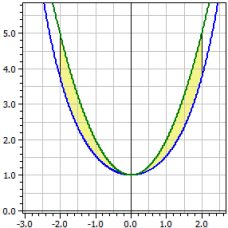
Ejemplo 2:
Longitud del arco de la línea de la cadena en comparación con la parábola normal y = x2 +1.
ƒ1 (x) = cosh (x)
ƒ2 (x) = x^2 + 1
Límites de integración de -2 a 2
Contenido orientado: A1 = -2,07961
Contenido absoluto: A2 = 2,07961
Longitudes de arco: L1 [a; b] = 7.254
L2 [a, b] = 9.294
Tenga en cuenta:
Las integrales se determinan mediante métodos numéricos. En principio, estos alcanzan sus límites con funciones con un cambio de signo muy rápido.
Ver también:
Funciones compatiblesAjuste de los gráficos

