Vector Product
Given two vectors the vector product and its magnitude are calculated.
The vector product is a vector orthogonal to the parallelogram formed by the given vectors. Its magnitude is equal to the area of the parallelogram.
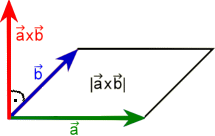
Example:
-> ⎧ 1 ⎫ -> ⎧ 7 ⎫
a = ⎪ 2 ⎪ b = ⎪ 1 ⎪
⎩ 3 ⎭ ⎩ 4 ⎭
-> -> ⎧ 5 ⎫ -> ->
a x b = ⎪ 17 ⎪ |a x b|= 21,977261
⎩-13 ⎭
Application:
Suppose you want to calculate the area of the triangle with vertices A(0|0|0), B(1|2|3) and C(7|1|4).
The triangle is half of the parallelogram that is spanned by the two vectors in the example. Its area is therefore half of their vector product A ≈ 11 area units.

