Triple Product
Given three vectors the program calculates the triple product. Its magnitude is equal to the volume of the parallelepipedon which is put up by the three vectors.
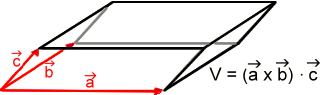
Linear dependent vectors has zero as triple product, because they lies in a plane
Example 1:
-> ⎧ 2 ⎫ -> ⎧ 2 ⎫ -> ⎧ 3 ⎫
a = ⎪ 3 ⎪ b = ⎪-1 ⎪ c = ⎪ 9 ⎪
⎩ 5 ⎭ ⎩ 7 ⎭ ⎩ 2 ⎭
-> -> ->
( a x b ) · c = 26
Example 2:
-> ⎧ 1 ⎫ -> ⎧ 2 ⎫ -> ⎧-1 ⎫
a = ⎪ 2 ⎪ b = ⎪ 1 ⎪ c = ⎪ 4 ⎪
⎩ 1 ⎭ ⎩ 1 ⎭ ⎩ 1 ⎭
-> -> ->
( a x b ) · c = 0
The three vectors are linear dependent.