Systems of Linear Equations

The program determines the solution vector of a system of linear equations (SLE) with n equations and n variables.

First enter then number of equations and then the coefficients of the system. The system must be transformed to :

a_1,1 ·x₁ + ... + a_1,n ·x_n = b₁

  :                                  :

a_n,1 ·x₁ + ... + a_n,n ·x_n = b_n

As an intermediate result the ref (Row Echelon Form) and the rref (Reduced Row Echelon Form) can be reported.

Example with unique solution:

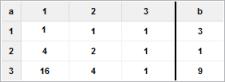
  1·x1 + 1·x2 + 1·x3  =   3
  4·x1 + 2·x2 + 1·x3  =   1
16·x1 + 4·x2 + 1·x3  =   9

L = { ( 2; -8; 9; ) }

Example with one-dim. solution:

 2·x1 + 3·x2 + 4·x3  =   0
 1·x1 − 1·x2 − 1·x3  =   1
 3·x1 + 2·x2 + 3·x3  =   1

L = { ( 0,6-0,2t; -0,4-1,2t; t ) | t ∈ R }        

Example with two-dim. solution:

 0·x1 + 0·x2 + 2·x3 − 1·x4  =  1
 1·x1 + 1·x2 + 1·x3 + 1·x4  =  4
 2·x1 + 2·x2 − 4·x3 + 5·x4  =  5
 1·x1 + 1·x2 − 7·x3 + 5·x4  =  0

L = { ( 3,5-s-1,5t; s; 0,5+0,5t; t ) | s,t ∈ R }

Demonstration for the first example:

If you are looking for a parabola through  P(1|3), Q(2|1) and R(4|9), you have to solve the following system of equations.

Approach:   f(x) = a·x² + b·x + c

The solution vector is:     (2, -8, 9)

Thus the parabola is discribed by   y = 2x² - 8x + 9.

Pop-up Menu:

Right click to open a local menu, which offers you the following functions to manage the matrix.

• Cut Matrix , Copy Matrix  and Paste Matrix

  With this you may copy the matrix to the clipboard and paste it into "Matrix multiplication".

• Export Matrix and Import Matrix

  Exports or imports the matrix in CSV format (Comma separated values), which is used to exchange data with Excel.