Binomial Distribution

For a b(k;n;p) distributed random variable X with fixed n and p you can calculate

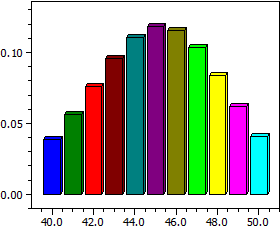
• a histogram of the probabilities P( X = k )
• a table of their values from k_min to k_max
• the probability P( k_min < X < k_max)

Theory:

n balls are drawn with replacement out of a container with a portion p of red balls. The random variable X stands for the amount of red balls drawn. The probability of k of the balls drawn being red, is characterized by P(X=k) = b(k;n;p).

The values for n and p are entered, where p as probability has to lie between 0 and 1. After this, a simple histogram gives a first survey over the values of P(X=k). The numeric values are issued in a table of values.

Example:

  n = 60;    p = .75

     k           P(X=k)          P(0 ≤ X < k)
  ——    ——————   ——————
    40      0,03834033      0,09248427 
    41      0,05610780      0,14859207 
    42      0,07614630      0,22473838 
    43      0,09562559      0,32036397 
    44      0,11083875      0,43120273 
    45      0,11822800      0,54943073 
    46      0,11565783      0,66508856 
    47      0,10335381      0,76844237 
    48      0,08397497      0,85241733 
    49      0,06169589      0,91411323 
    50      0,04071929      0,95483252 
  ——    ——————   ——————
  P(40 ≤ k < 50) =           0,90068858

See also:

Wikipedia: Binomial distribution