Combinatorial Analysis

Calculates the number of possibilities to select k out of n elements, if order matters or not (i.e. arrangement or combination), and permitting repetitions or not.

Example:

n = 49
k = 6

Arrangements without repetit. = 10 068 347 520
Arrangements with repetitions = 13 841 287 201
Combinations without repetit. = 13 983 816
Combinations with repetitions = 25 827 165

Permutations of k :        k! = 720

Formulas:

	Disorderd (Combinations)	Ordered (Variations)	Ordered and k=n (Permutations)
Without repetitions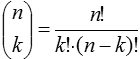
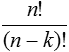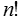With repetitions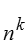

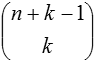In the urn model, selection with repetitions corresponds to drawing with replacement, and selection without repetitions corresponds to drawing without replacement. Ordered selection means that the balls are drawn one at a time, while unordered selection means they are drawn simultaneously.

See also:

Wikipedia: Enumerative combinatorics