Platonic solids
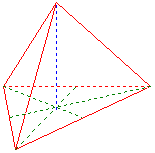
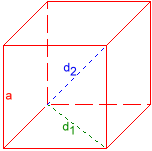
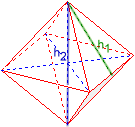
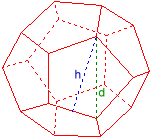
In Euclidean geometry, a Platonic solid is a convex polyhedron whose faces are congruent, regular polygons. It has been known since ancient times that there are exactly five Platonic solids :
Their names are derived from the number of faces and the Greek number names (Tetra=4, Hexa=6, Okta=8, Dodeka=12 and Ikosa=20):
Due to the high symmetry, one size (edge length, apothem, altitude, circumradius, inradius, volume or surface) is sufficient to fully determine the polyhedron.
Click on the corresponding figure for more details.