Special lines in a triangle
If the coordinates of the three vertices of a triangle are entered, the program calculates the equations of the perpendicular bisectors[1], of the side bisectors[2], of the angle bisectors[3] and of the altitudes[4]. In addition, the centers and radii of the circumcircle[5], of the incircle[6], of the three excircles[7] and the nine-point circle [8].
A list of check boxes can be used to select which objects are to be calculated and drawn.
 Perpendicular bisec.
Perpendicular bisec.
 Medians
Medians
 Angle bisectors
Angle bisectors
 Altitudes
Altitudes
 Incircle
Incircle
 Circumcircle
Circumcircle
 Excircles
Excircles
 Nine-point circle
Nine-point circle
Example 1: incircle and excircles of a triangle
Given:
¯¯¯¯¯¯
Vertices: A(1|0) B(5|1) C(3|6)
Results:
¯¯¯¯¯¯¯
Sides: a : 5·x + 2·y = 27
b : 3·x - y = 3
c : x - 4·y = 1
Incircle: Mi(3,119|1,962) r i = 1,390
Excircles: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
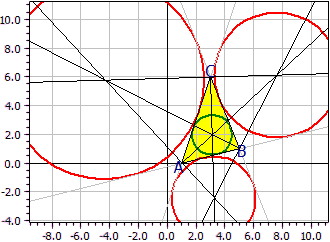
The center of the incircle (green) lies on the bisector of the three interior angles. The centers of the excircles (red) are each on the bisector of an inner angle and on the bisector of the outside angle of the other two triangle angles. These construction lines are also drawn.
Example 2: Altitudes in an obtuse-angled triangle
Given:
¯¯¯¯¯¯
Vertices: A(7|3) B(16|10) C(8|9)
Results:
¯¯¯¯¯¯¯
Sides: a : -x + 8·y = 64
b : 6·x - y = 39
c : 7·x - 9·y = 22
Altitudes: ha : 8·x + y = 59
hb : x + 6·y = 76
hc : 9·x + 7·y = 135
Altitudes feet: Ha(6,277|8,785)
Hb(8,378|11,27)
Hc(10,53|5,746)
Orthocenter: H(11,05|8,26)
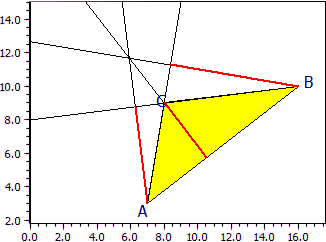
The intersection of the altitudes of an obtuse-angled triangle lies outside the triangle. The construction lines are also drawn. In order to make them more visible, the grid lines have been hidden.
Example 3: Excircles and nine-point circle
Given:
¯¯¯¯¯¯
Vertices: A(1|0) B(5|1) C(3|6)
Results
¯¯¯¯¯¯¯
Sides: a : 5·x + 2·y = 27
b : 3·x - y = 3
c : x − 4·y = 1
Excircles: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,91
Mc(3,248|-2,427) rc = 2,9
Nine-point circle: M9(3,295|2,068) r9 = 1,596
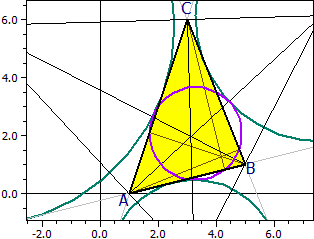
The nine-point circle touches the incircle and the excircles (Feuerbach's theorem)..
See also:
Setting the graphics
Wikipedia: Incircle and excircles |
Nine point circle


