Statistik
Zu einer Urliste werden der Mittelwert (arithmetisches Mittel), der Zentralwert (Median), die Varianz und die Standardabweichung bestimmt. Zusätzlich wird die Verteilung als Histogramm und Box-Plot ausgegeben.
Formeln:
Mittelwert: x = 1/n · Σ x(i) Varianz: s2 = 1/(n−1)·Σ(x(i) − x)2 bzw. 1/n·Σ(x(i) − x)2 Standardabw.: s = √s²
Beispiel:
Daten:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Anzahl der Daten n = 21
Maximum max = 11
Minimum min = 1
Mittelwert x = 7,7142857
Zentralwert c = 8
Varianz s² = 6,1142857
Standardabweichung s = 2,4727082
x H h
————————— ——— ——————
1 ≤ x < 2 1 0,047619
2 ≤ x < 3 0 0
3 ≤ x < 4 1 0,047619
4 ≤ x < 5 0 0
5 ≤ x < 6 1 0,047619
6 ≤ x < 7 2 0,0952381
7 ≤ x < 8 3 0,142857
8 ≤ x < 9 3 0,142857
9 ≤ x < 10 5 0,238095
10 ≤ x < 11 4 0,190476
Boxplot:
Q1=6,5; Q2=8; Q3=9,5; IQR=3
Left whisker=3; Right whisker=11
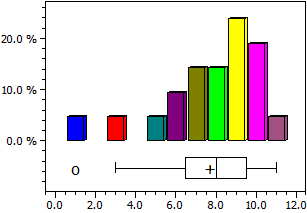
Der Box-Plot wird bestimmt durch die Quartile
Q1 : Median der unteren Datenhälfte (linker Rand der Box)
Q2 : Median aller Daten (Strich innerhalb der Box),
Q3 : Median der oberen Datenhälfte (rechter Rand der Box).
IQR = Q3−Q1 (Inter Qartile Range) ist die Breite der Box.
In diesem Bereich liegen 50% der Daten.
Die beiden Antennen (whisker) zeigen den kleinsten und den größten Wert, der nicht mehr als das 1,5-fache von IQR außerhalb der Box liegt.
Werte die nicht innerhalb dieses Bereichs liegen (Ausreißer) werden durch kleine Kreise gekennzeichnet.
Der Mittelwert wird durch ein Pluszeichen dargestellt.
Siehe auch:
Wikipedia: Varianz | Standardabweichung | Box-Plot

