Folgen und Reihen
Das Programm bestimmt die ersten n Glieder einer Folge (ai) und der zugehörigen Reihe (Summe der Folgenglieder), wenn die ersten Glieder der Folge und eine explizite Funktion ai=ƒ(i) oder eine Rekusrsionsformel ai=ƒ(a0, a1, ... , ai-1) gegeben sind.
Die Folge der ungeraden Zahlen
Sie kann explizit definiert werden durch ai = 2·i + 1 :
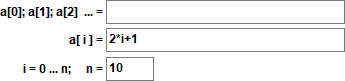
oder rekursiv durch ai = ai-1 + 2 mit a0=1 .

Folge ¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Reihe ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
Die zugehörige Reihe ist offensichtlich die Folge der Quadratzahlen. Das lässt sich sehr schön durch vollständige Induktion beweisen. ( Wikipedia: Vollständige Induktion / Summe_ungerader_Zahlen)
Die Fibonacci-Folge
Eine der bekanntesten rekursiven Folgen beginnt mit a0=1 und a1=1 . Die weiteren Gliedern sind jeweils gleich der Summe der beiden vorhergehenden.

Folge ¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Reihe ¯¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Siehe auch:
Wikipedia: Folge (Mathematik) | Fibonacci-Folge

