Distribuzione normale

Per una variabile casuale X distribuita di N(μ, σ ²) con la stima μ e la variante σ² , il programma traccia

 

- La funzione di densità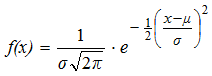    

- La funzione di distribuzione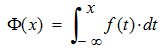  

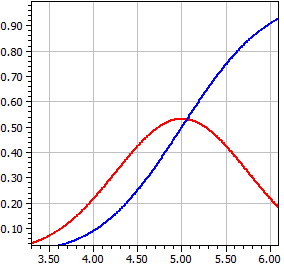
Il diagramma della funzione di densità f è spesso chiamato curva gaussiana o curva a campana a causa della sua forma. La funzione di distribuzione f è chiamata funzione di errore di Gauss perché approviamo questa distribuzione per errori accidentali nelle osservazioni astronomiche.

Inseriamo la stima μ e la variante σ² . Per μ=0  e  σ=1 riceviamo la distribuzione normale ridotta.

Esempio:

  μ = 5 ,      σ = .75

         x                     ƒ(x)                   Φ(x)      
  —————       –—————     —————–
  2                       0,00017844      0,00003167   
  2,33333333      0,00095649      0,00018859
  2,66666666      0,00420802      0,00093192
  2,99999999      0,01519465      0,00383038
  3,33333332      0,04503153      0,01313415
  3,66666665      0,10953585      0,03772017
  3,99999998      0,21868009      0,09121120
  4,33333331      0,35832381      0,18703139
  4,66666664      0,48189843      0,32836063
  4,99999997      0,53192304      0,49999998
  5,3333333        0,48189845      0,67163934
  5,66666663      0,35832383      0,81296859
  5,99999996      0,21868012      0,90878878
  6,33333329      0,10953586      0,96227982

Vedi anche:

Wikipedia: Distribuzione normale