Statistica
Viene fornito un elenco di osservazioni, vengono determinati il valore medio (aritmetico), la mediana, la variante e la deviazione standard. Inoltre, la distribuzione viene emessa dall'istogramma e una diagramma a scatola e baffi.
Formule:
Valore medio: x = 1/n · Σ x(i) Variante: s2 = 1/(n−1)·Σ(x(i) − x)2 bzw. 1/n·Σ(x(i) − x)2 Deviazione standard.: s = vs²
La mediana è il valore al centro dell'elenco delle osservazioni. Con un numero pari di valori, la mediana è il valore medio dei due valori centrali.
Esempio:
Daten:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Numero di date n = 21
Maximum max = 11
Minimum min = 1
Valore medio x = 7,7142857
Mediana c = 8
Variante s² = 6,1142857
Deviazione standard s = 2,4727082
x H h
————————— ——— ——————
1 ≤ x < 2 1 0,047619
2 ≤ x < 3 0 0
3 ≤ x < 4 1 0,047619
4 ≤ x < 5 0 0
5 ≤ x < 6 1 0,047619
6 ≤ x < 7 2 0,0952381
7 ≤ x < 8 3 0,142857
8 ≤ x < 9 3 0,142857
9 ≤ x < 10 5 0,238095
10 ≤ x < 11 4 0,190476
Boxplot:
Q1=6,5; Q2=8; Q3=9,5; IQR=3
Left whisker=3; Right whisker=11
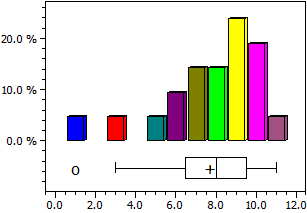
La diagramma a scatola è determinato dai quartili
Q1: mediana della metà inferiore dei dati (bordo sinistro della scatola)
Q2: mediana di tutti i dati (riga all'interno della scatola),
Q3: mediana della metà superiore dei dati (bordo destro della scatola).
IQR = Q3-Q1 (InterQartile Range) è la larghezza della scatola.
Il 50% dei dati si trova in quest'area.
Le due baffi (whiskers) mostrano il valore più piccolo e quello più grande, che non è più di 1,5 volte l'IQR fuori della scatola.
I valori che non rientrano in questo intervallo (valori anomali) sono indicati da piccoli cerchi.
Il valore medio è rappresentato da un segno più.

