Statistiques
Une liste des observations est donnée, la valeur moyenne (arithmétique), la médiane, la variante et l'écart type sont déterminés. En supplément la distribution est sortie par histogramme.
Formules:
Valeur moyenne: x = 1/n · Σ x(i) Variante: s2 = 1/(n−1)·Σ(x(i) − x)2 bzw. 1/n·Σ(x(i) − x)2 Ecart-type: s = √s²
La Médiane est la valeur au centre de la liste des observations. Avec un nombre paire des valeurs, la médiane est la valeur moyenne des deux valeurs centrales.
Exemple:
Dates:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Nombres des dates n = 21
Maximum max = 11
Minimum min = 1
Valeur moyenne x = 7,7142857
Médiane c = 8
Variante s² = 6,1142857
Ecart-type s = 2,4727082
x H h
————————— ——— ——————
1 ≤ x < 2 1 0,047619
2 ≤ x < 3 0 0
3 ≤ x < 4 1 0,047619
4 ≤ x < 5 0 0
5 ≤ x < 6 1 0,047619
6 ≤ x < 7 2 0,0952381
7 ≤ x < 8 3 0,142857
8 ≤ x < 9 3 0,142857
9 ≤ x < 10 5 0,238095
10 ≤ x < 11 4 0,190476
Boxplot:
Q1=6,5; Q2=8; Q3=9,5; IQR=3
Left whisker=3; Right whisker=11
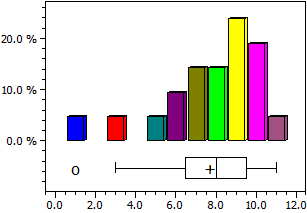
Le box plot est déterminé par les quartiles
Q1: Médiane de la moitié inférieure des données (bord gauche de la boîte)
Q2: Médiane de toutes les données (ligne dans la boîte),
Q3: Médiane de la moitié supérieure des données (bord droit de la boîte).
IQR = Q3-Q1 (InterQartile Range) est la largeur de la boîte.
50% des données se trouvent dans ce domaine.
Les deux moustaches (whiskers) affichent la valeur la plus petite et la plus grande, qui ne sont plus que 1,5·IQR à l'extérieur de la boîte.
Des valeurs qui ne sont pas comprises dans cette plage (valeurs aberrantes) sont indiquées par de petits cercles.
La valeur moyenne est représentée par un signe plus.

