Calcul intégral

La surface orientée et la surface absolue entre deux courbes dans un intervalle choisit sont calculées.

En outre le programme détermine :

• Les moments de rotation aux environs des axes des x et l'axe de y,
• les corps de révolution,
• les longueurs d'arc dans l'intervalle [a;b] et
• le centre de gravité de la zone (si A1=A2).

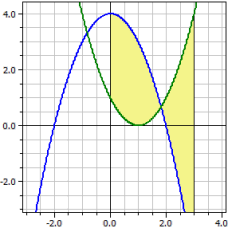
Exemple 1:

  ƒ1(x) = 4-x^2
  ƒ2(x) = (x-1)^2

  Intervalle d'intégration de  0  à  3

  Surface orientée       :  A1 = 0,00000
  Surface absolue        :  A2 = 9,50675

  Moments de rotation :  Mx = 9               My = -9

  Corps de révolution  :  Vx = 56,5487     Vy = -56,5487

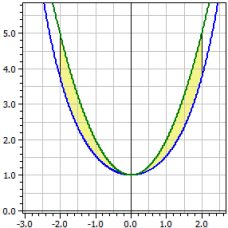
Exemple 2:

Longueur d'arc de la ligne de chaîne par rapport à la parabole normale  y=x²+1.

  ƒ1(x) = cosh(x)
  ƒ2(x) = x^2+1

  Intervalle d'intégration de  -2  à  2

  Surface orientée    :  A1 = -2,07961
  Surface absolue     :  A2 = 2,07961

  Longueur d'arc      :  L1[a;b] = 7,254      L2[a,b] = 9,294

Notez s'il vous plaît:

Les intégrales sont déterminées à l'aide de méthodes numériques. En principe, ceux-ci atteignent leurs limites avec des fonctions avec un changement de signe très rapide.

Voir aussi:

Fonctions soutenu
Ajuster des graphiques