Itération de Newton
L'itération de Newton est une méthode d'approximation pour calculer les zéros de ƒ(x). Donner une valeur initiale x0, assez prêt du nul cherché, l'approximation prochaine est calculée par l'intersection de la tangente de ƒ dans le point P(x0|ƒ(x0)) avec l'axe horizontal.
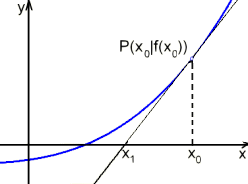
De cela résulte la formule de récurrence.
La méthode convergente, si ƒ(x0) · ƒ "(x0)>0
est valide pour x0.
Exemple:
ƒ(x) = x-cos(x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Voir aussi:
Fonctions soutenuWikipedia: Méthode de Newton

