Polygones arbitraires
D'abord les coordonnées des points du sommets d'un polygone doivent être entrées.
Après cela, l'aire, la circonférence et les coordonnèes des centres de gravités (respéctivement aux points ou l'aire), sont montrés et le polygone est dessiné.
Les côtés et les angles du polygone sont également calculés et il est vérifié si le polygone est convexe, concave ou croisé.
Polygone convexe:
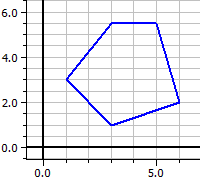
Polygone concave:
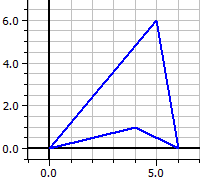
Polygone croisé:
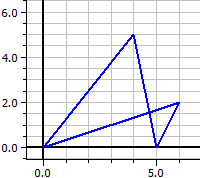
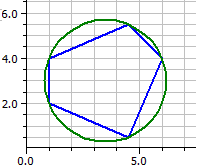
De plus, les polygones convexes sont vérifiés s'ils ont un cercle inscrit et/ou un cercle circonscrit.
Polygone tangent:
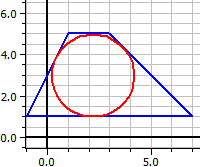
Polygone inscribtible:
Exemple:
Points: Aire A = 18
A(0|0)
B(4|1) Circonférence p = 22,032567
C(6|0)
D(5|7) Centre de gravités de points:
CP(3,75|2)
Centre de gravités de l'aire:
CA(3,72222|2,66667)
Côtés: Angles:
|AB| = 4,1231056 ∡BAD = 36,158185°
|BC| = 2,236068 ∡CBA = 220,60129°
|CD| = 6,0827625 ∡DCB = 53,972627°
|DA| = 7,8102497 ∡ADC = 49,267893°
Polygone concave
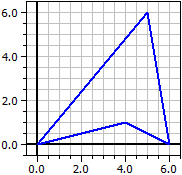
∡BAD est l'angle de rotation du rayon [AB[
dans le sens antihoraire par rapport à [AD[.

