Lignes spéciales dans un triangle
Si les coordonnées des trois sommets d'un triangle sont saisies, le programme calcule les équations des bissectrices perpendiculaires [1], des medianes[2], des bissectrices d'angle[3] et des altitudes[4]. De plus, les centres et les rayons du cercle circonscrit[5], du cercle inscrit[6], des trois cercles exinscrits[7] et du cercle d'Euler [8].
Une liste des check boxes peut être utilisée pour sélectionner les objets à calculer et à dessiner.
 Médiatrices
Médiatrices
 Medianes
Medianes
 Bissectrices
Bissectrices
 Hauteurs
Hauteurs
 Cercle inscrit
Cercle inscrit
 Cercle circonscrit
Cercle circonscrit
 Cercles exinscrit
Cercles exinscrit
 Cercle d'Euler
Cercle d'Euler
Exemple 1: Cercle inscrit et cercle exinscrit d'un triangle
Entrées:
¯¯¯¯¯¯¯
Sommets: A(1|0) B(5|1) C(3|6)
Résultats:
¯¯¯¯¯¯¯¯
Côtés: a : 5·x + 2·y = 27
b : 3·x - y = 3
c : x - 4·y = 1
Cercle inscrit: Mi(3,119|1,962) r i = 1,390
Cercles exinscrit: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
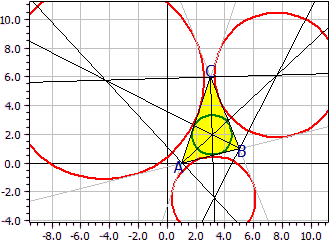
Le centre de cercle inscrit (vert) se trouve sur la bissectrice des trois angles intérieurs. Les centres des cercles exinscrits (rouges) sont chacun sur la bissectrice d'un angle intérieur et sur la bissectrice de l'angle extérieur des deux autres angles. Ces lignes de construction sont également dessinées.
Exemple 2: Altitudes dans un triangle à angle obtus
Entrées:
¯¯¯¯¯¯¯
Sommets: A(7|3) B(16|10) C(8|9)
Résultats:
¯¯¯¯¯¯¯¯
Côtés: a: -x + 8y = 64
b: 6x - y = 39
c: 7x - 9y = 22
Altitudes: ha: 8x + y = 59
hb: x + 6y = 76
hc: 9x + 7y = 135
Pts. de base: Ha(6,277|8,785) Hb(8,378|11,27)
Hc(10,53|5,746)
Orthocentre: H(11.05|8.26)
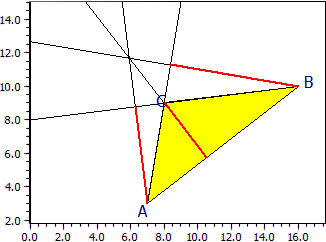
L'intersection des altitudes d'un triangle à angle obtus se situe à l'extérieur du triangle. Les lignes de construction sont également dessinées. Afin de les rendre plus visibles, les lignes de la grille ont été masquées.
Exemple 3: Cercles exinscrit et cercle d'Euler
Entrées:
¯¯¯¯¯¯¯
Sommets: A(1|0) B(5|1) C(3|6)
Résultats:
¯¯¯¯¯¯¯¯
Côtés: a : 5·x + 2·y = 27
b : 3·x − y = 3
c : x − 4·y = 1
Cercles exinscrit: Ma(7,626|6,136) ra = 4,346
Mb(-4,356|5,784) rb = 6,910
Mc(3,248|-2,427) rc = 2,900
Cercle d'Euler: M9(3,295|2,068) r9 = 1,596
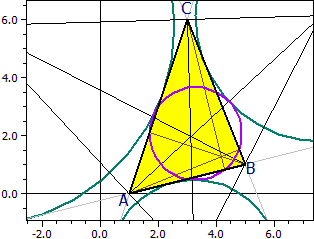
Le cercle d'Euler touche le cercle inscrit et les cercles exinscrit (théorème de Feuerbach).
Voir aussi:
Ajuster des graphiques
Wikipédia: Cercles inscrit et exinscrits d'un triangle |
Cercle d'Euler


