Triangles par 3 grandeurs
Des triangles sont déterminés par trois grandeurs extérieur (côtés ou angles) si l'une des congruences suivantes sont remplies:
- sss trois côtés sont données.
- sww un côté et deux angles sont donnés.
- sws deux côtés et l'angle fermé sont données
- Ssw deux côtés et l'angle opposé de la grande côté sont donnés.
Si on entre 3 grandeurs, extérieures d'un triangle (des côtés ou des angles) le programme calcul les autres côtés, les angles, les hauteurs, les médianes, les bisséctrices, la circonférence et l'aire.
En plus les centre et rayon du cercle inscrit et du cercle circonscrit. En outre les triangles avec cercle inscrit et circonscrit sont dessinés.
Si on entre 2 côtés et l'angle opposé au côté plus petit il y a peut-être 2 solutions.
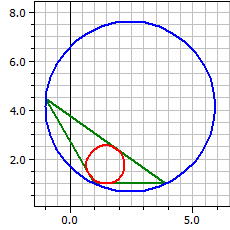
Exemple 1:
Entrées: a = 6, b = 4, α=60°
Sommets: A(1|1) B(7,899|1) C(3|4,4641)
Côtés: 6 4 6,89898
Angles: 60° 35,2644° 84,7356°
Hauteurs: 3,98313 5,97469 3,4641
Médians: 4,77472 6,148 3,75513
Bisséctr.: 4,38551 6,11664 3,5464
C.circon.: M(4,44949|1,31784) ru = 3,4641
C.inscrit : O(3,44949|2,41421) ri = 1,41421
Aire: A = 11,9494 Périmetre u = 16,899
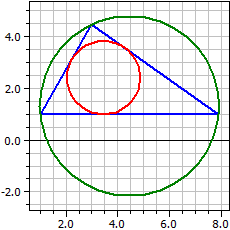
Exemple 2:
Entrées: a = 6, b = 4, β = 35,2644
1ere solution:
Sommets: A(1|1) B(7,899|1) C(3|4,464)
Côtés: 6 4 6,89898
Angles: 60° 35,2644° 84,7356°
Hauteurs: 3,98313 5,97469 3,46410
Médians: 4,77472 6,14800 3,75513
Bisséctr.: 4,38550 6,11664 3,5464
C.circon.: M(4,449|1,3178) ru = 3,4641
C.inscrit: O(3,449|2,4142) r i = 1,41421
Aire: A = 11,9494 Périmetre u = 16,899
—————————————————————
2e solution:
Sommets: A(1|1) B(3,899|1) C(-1|4,464)
Côtés: 6 4 2,89898
Angles: 120° 35,2644° 24,7356°
Hauteurs: 1,67373 2,51059 3,46410
Médians: 1,78943 4,26639 4,88866
Bisséctr.: 1,68082 3,72554 4,68861
C.circon.: M(2,449|4,146) ru = 3,4641
C.inscrit: O(1,449|1,779) r i = 0,7785
Aire: A = 5,0212 Périmetre u = 12,899