Estadísticas
La media (media aritmética), la mediana, la varianza y la desviación estándar se determinan para una notación prima. además, la distribución se presenta como un histograma.
Fórmulas:
Media: x = 1/n · Σ xi Varianza: s2 = 1/(n − 1) · Σ (xi - x )2 resp. 1/n · Σ (xi - x )2 Desv. estándar: s = √ s²
La mediana es ese valor, que se encuentra en el medio de la lista ordenada. En el caso de un número par de valores, la mediana es la media de los dos valores en el medio de la lista.
Ejemplo:
Datos:
9 6 7 7 3 9 10 1 8 7 9 6 9 8 10 5 10 10 9 11 8
Número de datos n = 21
Máximo max = 11
Mínimo min = 1
Media x = 7,7142857
Mediana c = 8
Varianza s2 = 6,1142857
Desviación estándar s = 2,4727082
x H h
—————— ——— —————
1 ≤ x <2 1 0,047619
2 ≤ x <3 0 0
3 ≤ x <4 1 0,047619
4 ≤ x <5 0 0
5 ≤ x <6 1 0,047619
6 ≤ x <7 2 0,0952381
7 ≤ x <8 3 0,142857
8 ≤ x <9 3 0,142857
9 ≤ x <10 5 0,238095
10 ≤ x <11 4 0,190476
Diagrama de caja:
Q1 = 6,5; Q2 = 8; Q3 = 9,5; IQR = 3
Bigote izquierdo = 3; Bigote derecho = 11
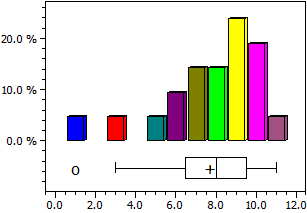
El diagrama de caja (box plot) está determinado por los cuartiles
Q1: Mediana de la mitad inferior de los datos (borde izquierdo del cuadro)
Q2: Mediana de todos los datos (línea dentro del cuadro),
Q3: Mediana de la mitad superior de los datos (derecha borde de la caja).
IQR = Q3-Q1 (InterQartile Range) es el ancho de la caja.
El 50% de los datos se encuentran en esta área.
Los dos bigotes (whiskers) muestran el valor más pequeño y más grande, que no es más de 1,5 veces el IQR fuera de la caja.
Los valores que no están dentro de este rango (valores atípicos) se indican mediante círculos pequeños.
El valor medio está representado por un signo más.

