Iteración de Newton
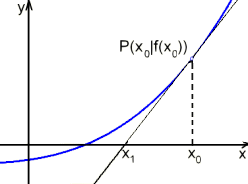
La iteración de Newton es un método de aproximación para el cálculo de un cero de ƒ(x). Si se ingresa un valor inicial x0 , que está lo suficientemente cerca del cero deseado, entonces la siguiente aproximación calculada es la intersección de la tangente a la gráfica de ƒ en el punto P (x0 | ƒ(x0)) con el eje x.
Esto conduce a la fórmula de recursividad.
El procedimiento converge si ƒ(x0)·ƒ "(x0)> 0
es válido para x0 .
Ejemplo:
ƒ(x) = x − cos (x)
x ƒ(x) ƒ'(x)
———————— —————— ——————
x0 = 1
x1 = 0,75036387 0,45969769 1,841471
x2 = 0,73911289 0,018923074 1,681905
x3 = 0,73908513 0,00004646 1,6736325
x4 = 0,73908513 0,00000000 1,673612
Ver también:
Funciones compatiblesWikipedia: Método de Newton

