Secuencias y series
El programa determina los primeros n términos de una secuencia (ai) y la serie asociada (suma de los términos de la secuencia) si los primeros términos de la secuencia y una función explícita ai = ƒ(i) o una fórmula de recurso ai = ƒ(a0 , a1 , ..., ai-1 ) se dan.
La secuencia de números impares
Puede definirse explícitamente con ai = 2·i + 1:
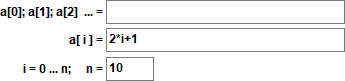
o recursivamente con ai = ai-1 + 2 con a0 = 1.

Secuencia ¯¯¯¯¯¯¯¯¯ (a [i]) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Serie ¯¯¯¯ (Σ a [i]) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
La serie correspondiente es obviamente la secuencia de los números cuadrados. Esto se puede probar muy bien por inducción completa.
La secuencia de Fibonacci
Una de las secuencias recursivas más populares comienza con a0 = 1 y a1 = 1. Los otros términos son iguales a la suma de los dos anteriores.

Secuencia ¯¯¯¯¯¯¯¯¯ (a[i]) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Serie ¯¯¯¯ (Σ a[i]) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
Ver también:
Wikipedia: Sucesión | Sucesión de Fibonacci

