Sequences and series
The program calculates the first n terms of a sequence (ai) and the corresponding series (sum of the sequence terms) if the first terms of the sequence and an explicit function ai=ƒ(i) or a recourse formula ai=ƒ(a0, a1, ... , ai-1) are given.
The sequence of odd numbers
It can be defined explicitly by ai = 2·i + 1 :
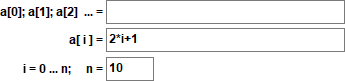
or recursively by ai = ai-1 + 2 with a0=1 .

Sequence ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 3; 5; 7; 9; 11; 13; 15; 17; 19) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 4; 9; 16; 25; 36; 49; 64; 81; 100)
The corresponding series is obviously the sequence of the square numbers. This can be proved very nicely by complete induction. ( Wikipedia: Mathematical induction / Sum of consecutive natural numbers )
The Fibonacci Sequence
One of the most popular recursive sequences starts with a0=1 and a1=1 . The other terms are equal to the sum of the previous two.

Sequence ¯¯¯¯¯¯¯¯ ( a[ i ] ) = (1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144; 233; 377; 610; 987; 1597; 2584; 4181; 6765) Serie ¯¯¯¯ ( Σ a[ i ] ) = (1; 2; 4; 7; 12; 20; 33; 54; 88; 143; 232; 376; 609; 986; 1596; 2583; 4180; 6764; 10945; 17710)
See also:
Wikipedia: Sequence | Fibonacci number

