Transformation of polynomials
A polynomial p(x) can be shifted or stretched in the x-direction and the y-direction.
p(x) = a9·x9 + a 8·x8 + ... + a0 .
The coefficients of the polynomial can be entered as fractions, as mixed numbers or as decimal numbers.

ƒ(x) = - 1/4·x4 + 2·x3 - 16·x + 21 Shifted by dx = -2, dy = 0 ƒ(x + 2) = - 1/4 ·x4 + 6 ·x2 + 1
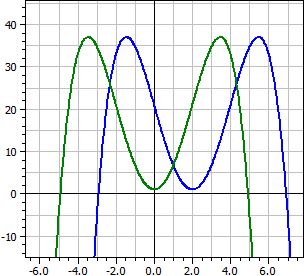
In the example, the function ƒ(x) has the axis of symmetry a: x = 2. By moving 2 steps to the left we get the function ƒ(x + 2), which is symmetric about the y-axis and therefore only has summands with even powers of x.
Data exchange via the Windows clipboard
All program parts in which the coefficients of a polynomial are entered have a context menu (right mouse button) with which you can copy the entries from one program part to the clipboard and paste them from there into another program part.
The coefficients of the transformed function are automatically copied to the clipboard.
In this way, the functions ƒ(x) and ƒ(x + 2) have been copied by copy and paste to the function plotter . The paste function automatically converts the coefficient table into the function term.
Further examples:
ƒ(x) = x5 + 10·x4 + 36·x3 + 56·x2 + 33·x + 3 Shifted by dx = 2, dy = 1 ƒ(x -2) + 1 = x5 - 4·x3 + x + 2
ƒ(x) = 1/4·x4 + 2·x2 - 1 Stretched by sx = 2, sy = 1 ƒ(1/2·x) = 1/64·x4 + 1/2·x2 - 1
ƒ(x) = 1/4·x4 + 2·x2 - 1 Stretched by sx = 1/2, sy = 3 3·ƒ(2·x) = 12·x4 + 24·x2 - 3
ƒ(x) = x5 - 9·x4 - 82/9·x3 + 82·x2 Stretched by sx = -1, sy = 9 9·ƒ(-1x) = - 9·x5 - 81·x4 + 246·x3 + 738·x2

