Coordinate Systems
With this you can convert three-dimensional Cartesian coordinates to three-dimensional polar or cylindrical coordinates and vice versa.
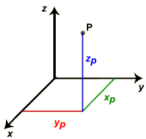
Cartesian coordinates
In a Cartesian coordinate system (x|y|z) a point is located by its distance from each of three mutually perpendicular intersecting lines with the same unit of length.
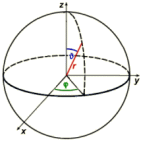
Polar coordinates
In a polar coordinate system (r|φ|Θ) a point is located by its radius vector, the rotation angle φ (phi) on the equatorial plane and the elevation angle Θ (theta) from the equatorial plane.
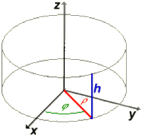
Cylindrical coordinates
In a cylindrical coordinate system (ρ|φ|z) a point is located by its distance ρ (rho) from the cylinder axis, the rotation angle φ (phi) around the axis and the altitude z above the origin.
Example:
cartesian polar cylindrical x = 1 r = 1.7320508 ρ = 1.4142136 y = 1 φ = 45° φ = 45° z = 1 Θ = 35,26439° z = 1

