Tangent lines to circles - Calculation
Pole and Polar
The circle k around the center M with radius r is described by the equation
(x - xM)2 + (y - yM)2 = r2 .
If you insert the coordinates of point P into one of the factors in the squares on the left, you get the following equation, which describes a straight line.
(xP - xM)·(x - xM) + (yP - yM)·(y - yM) = r2 .
It is called the polar to the pole P and is a powerful tool for finding the tangent equations.
The tangents to a circle k through a point P.
Given a circle k and a point P on the circle, the polar of P is the desired tangent
Given a circle k and a point P outside of k, the polar of P intersects the circle at the two points of contact of the tangents through P. The equation of the polar is solved for y (or for x if the coefficient of y is zero) and inserted into the circular equation. With the contact points B1 and B2 calculated in this way, the equations of the tangents t1 = (PB1) and t2 = (PB2) are set up.
If the point P is inside the circle, the polar is a straight line outside the circle. The points on it all have the property that their polar intersect in P.
The tangents to a circle k parallel to a straight line g
Given a circle k and a straight line g: a x + b y = c , the perpendicular to g through the center M of the circle intersects it at the contact points B1 and B2 . For the coefficients of the perpendicular line applies a '= - b and b' = a. The constant summand c' is obtained by inserting the coefficients of M.
Tangents to two circles k1 and k2
If r1 and r2 are the radii of the circles k1 and k2, we assume w.l.o.g. that r1>r2. If not, the circles are swapped.
How many common tangents two circles have depends on the mutual position of the circles:

|M1M2| < r1 − r2

|M1M2| = r1 − r2

r1 − r2 < |M1M2| < r1 + r2

|M1M2| = r1 + r2
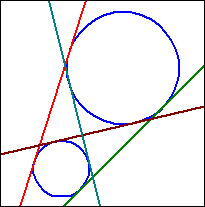
|M1M2| > r1 + r2

Special case r1 = r2
a) |M1M2| = r1 − r2
The easiest way to calculate the common contact point B is to add the r2/|M1M2|-fold of the vector from M1 to M22 to the position vector of M2. The tangent is the perpendicular to (M1M2) in B.
b) |M1M2| > r1 − r2
In order to determine the outer tangents to two circles, one first determines the tangents from M2 to a circle k3 around M1
with radius r3 = r1 − r2 (analogous to "Tangent to k through P"). If P1 and P2 are the contact points on k3,you may shift them by r1/r3 times the vector from M1 to P1 or P2 resp. in order to get the contact points B1 and B2 (cf. a)).
Two circles with the same radius form a special case, since the auxiliary circle k3 would have a radius of zero. In this case the tangents are determined analogously to "Tangent to k parallel to g" with g = (M1M2).
c) |M1M2| = r1 + r2
If the two circles touch from outside, there is a third common tangent t3 . The common point of contact divides the distance M1 M2 in the ratio r1:r2. The tangent t3 is orthogonal to M1M2.
d) |M1M2| > r1 + r2
If k2 is completely outside k1, there are two "inner" common tangents that cross between the circles.
In order to determine the inner tangents to two circles, one first determines the tangents from M2 to a circle k3 around M1
with radius r3=r1+r2 (analogous to "Tangent to k through P").
If P1 and P2 are the contact points on k3, then these are shifted by r1/r3 times the vector
from M1 to P1 or P2 resp. (cf. a)).

